Thermomechanical coupling of phase transformations and constitutive laws to describe microstructural evolution of substitutional solder alloys
 Wolfgang Flachberger¹ | Thomas Antretter¹ | Jiri Svoboda² | Silvia Leitner³ | Manuel Petersmann⁴
Wolfgang Flachberger¹ | Thomas Antretter¹ | Jiri Svoboda² | Silvia Leitner³ | Manuel Petersmann⁴
¹ University of Mining, Leoben, Austria | ² Institute of Physics of Materials - Academy of Sciences of the Czech Republic | ³ Materials Center Leoben Forschung GmbH | ⁴ Kompetenzzentrum Automobil- und Industrieelektronik GmbH
Lars Onsager

- Born in Oslo
- One of the most important contributors of "Nonequilibrium Thermodynamics"
- He discovered the "Onsager reciprocal relations"
Onsager reciprocal relations
\[ \mathcal{P} = \underline{j}_i \; \underline{\underline{L}}_{ik} \; \underline{j}_k \]"everything is coupled."
The principle of minimum entropy production..
..or maximum entropy production?
\[ \delta (\dot{\mathcal{F}} + \tfrac{T}{2} \mathcal{P}) = 0 \]The free energy of the Cahn-Hilliard model
\[ \mathcal{F}[c] = \frac{1}{\Omega} \int_{V} f_0(c) + \frac{\kappa}{2} | \nabla c |^2 \; dV \]The molar free energy in a stress free system
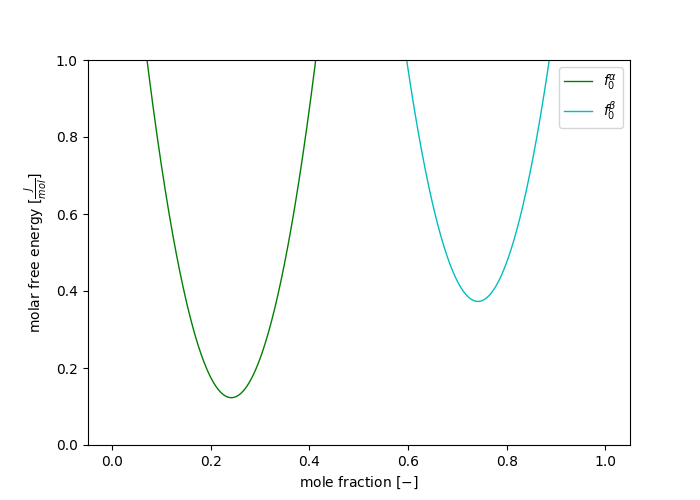
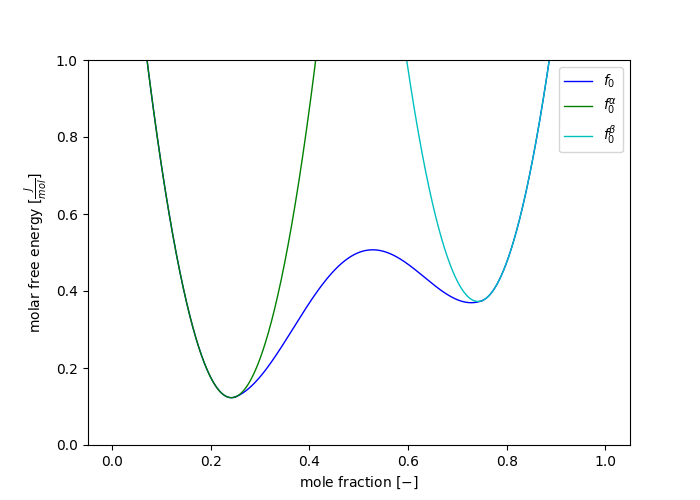
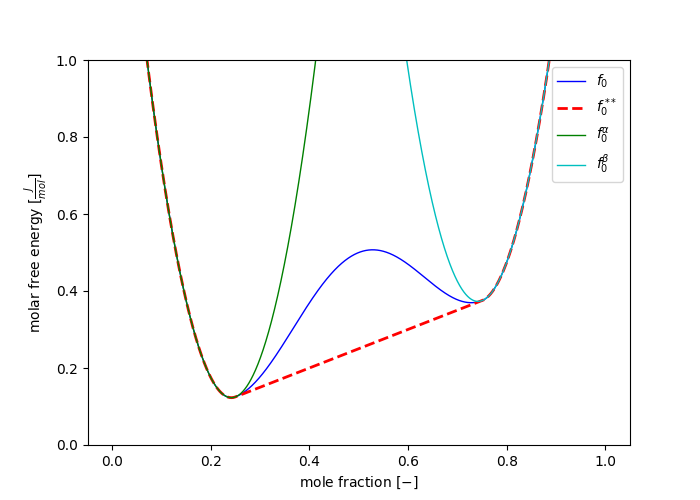
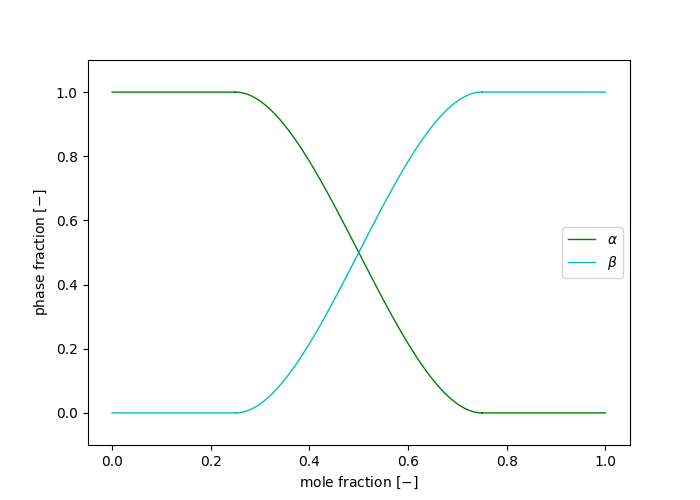
A free energy functional with additional strain energy
\[ \mathcal{F}[c,\underline{u}] = \frac{1}{\Omega} \int_{V} f_0(c) + \frac{\kappa}{2} | \nabla c |^2 + \varphi(c,\underline{u}) \; dV \]A Lagrangian for the Thermodynamic Extremal Principle
Euler-Lagrange Equations
Variational Formulation
\[\begin{aligned} 0 & = \int_{V} \Big( \frac{1}{\Omega} \frac{\partial \psi(c,\underline{u})}{\partial c} + \bar{\mu} \Big) \hat{c} \; dV \;\;\;\;\; \forall \; \hat{c} \in D^0 \\ 0 & = \int_{V} \Big( \frac{T}{L} \underline{j} \cdot \underline{\hat{j}} + \bar{\mu} \Omega \nabla \cdot \underline{\hat{j}} \Big) \; dV \;\;\;\;\; \forall \; \underline{\hat{j}} \in R^1 \\ 0 & = \int_{V} \big( \frac{c - c_t}{\Delta t} + \Omega \nabla \cdot \underline{j} \big) \hat{\bar{\mu}} \; dV \;\;\;\;\; \forall \; \hat{\bar{\mu}} \in D^0 \\ 0 & = \int_{V} \sigma(c,\underline{u}) : \nabla_s \hat{\underline{u}} \; dV \;\;\;\;\; \forall \; \hat{\underline{u}} \in C^2 \end{aligned} \] https://fenicsproject.org/olddocs/dolfin/1.5.0/python/demo/documented/mixed-poisson/python/documentation.htmlThe End.
Thank you for your attention. For more information on my work visit https://preprint.flachberger.online
